The other day, someone asked me if I were stranded on a desert island and could take only one data structure with me, what would I choose?
Without a second thought, I said Hash Tables.
Okay, I wasn’t asked this question, but Peter Van Der Linden, Author of Deep C Secrets was.
But, hey, at least we share the same spirit and obviously the same answer.
Curious why we chose this structure? Read along.
Arrays with Meaningless Indexes:
When we spoke about arrays, we’ve used a numeric index to access our element. But, with hash tables, we widen our option and use meaningful keys to add or access each element.
Let’s take a small example to discover hidden meaning in above sentences.
Assume we want to store the names of few states in India. A simple array of strings can easily accomplish this task.
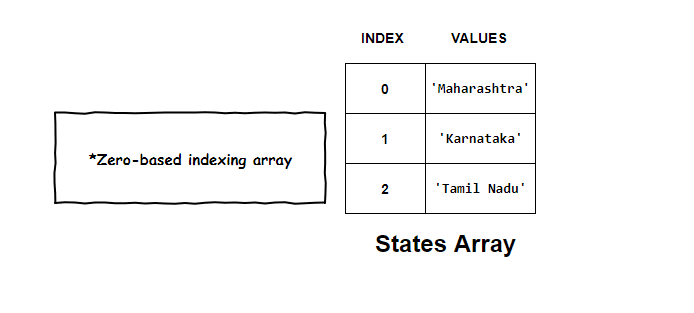 With each element of the array, came its own index number. This indexed superpower of arrays helped us access each element independently.
With each element of the array, came its own index number. This indexed superpower of arrays helped us access each element independently.
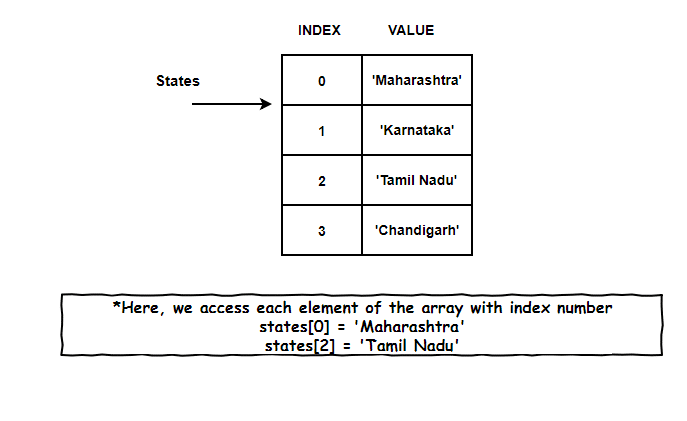 But, have you ever wondered what’s with these boring index numbers. Why can’t I replace them with Marvel superheroes name? Or something more meaningful which can establish a relationship between the index of an array and its element.
But, have you ever wondered what’s with these boring index numbers. Why can’t I replace them with Marvel superheroes name? Or something more meaningful which can establish a relationship between the index of an array and its element.
Going From Meaningless Zero-Based Indexing to Meaningful Indexes:
Boring Index numbers out, meaningful Abbreviations a.k.a Keys in.
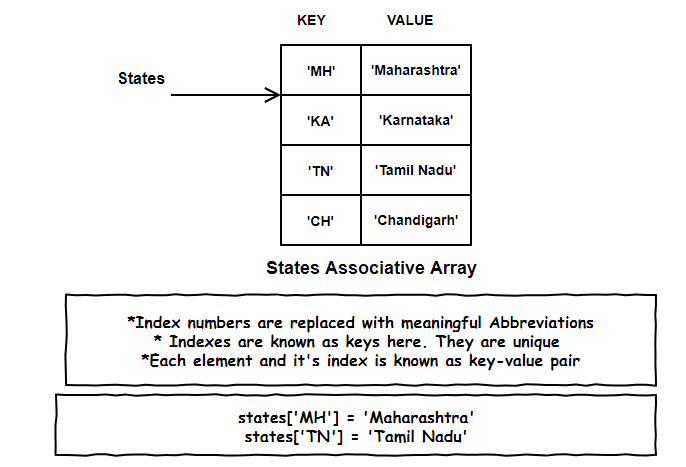 This kind of meaningful indexed array is known as an Associative array. Remember those boring index nos, they are re-branded as keys here.
This kind of meaningful indexed array is known as an Associative array. Remember those boring index nos, they are re-branded as keys here.
So, each element and its respective index is known as a key-value pair. And just like array indexes, keys in associative array needs to be unique.
Same Thing, Different Names:
The practical implementation of associative arrays has different names in different programming languages. In some languages, they are called a dictionary. Or Maps. Or Hash.
 I know at these moment many questions would have raised in your mind like:
I know at these moment many questions would have raised in your mind like:
- All associative array did was add additional key, why bother using it instead of a beloved array?
- And weren’t we on hash tables? Why on earth are we discussing multi-named associative array? Phew! I’ll start with question number two:
Associative arrays or Maps or Dictionaries are implemented using Hash Tables. So, we are so on the same topic.
Now, for question No 1, we will have to revisit our problems faced by our beloved array in the previous article and see how hash tables solves them.
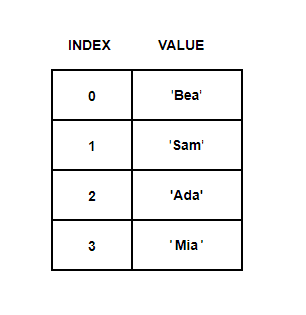
Let’s say we’ve have a simple one-dimensional array and we want to find if our array has string ‘Sam’ in it.
arr = ['Ada', 'Bea', 'Sam', 'Mia']
Linear Search:
We’ve to perform a linear search on our array i.e visiting each and every single element of an array to see if string ‘Sam’ exists.
But, what if the array is holding thousands of data?
The time taken to search is directly related to how many data we have which is linear time or O(n).
Sure, we can perform sorting and try to get down the complexity to O(log n), but we also know sorting is computing intensive.
(Read how to calculate algorithm complexity here)
We’ve hit a wall now.
But, remember, there are always two doors, one to hell and other to heaven.
Our Heaven Door:
But, what if some angel falls from the sky and tells you, “Ah, the string ‘Sam’ is located at array index 2.
And Voila!
From linear time O(n), our complexity drops to constant time O(1).
Just by knowing the index, the size of the array and the position of the element in the array doesn’t matter even if we’ve thousands of data.
But, the ultimate question to be answered now: how do we know or calculate where our element resides.
Hash Tables To the Rescue.
What are Hash Tables in Data Structures?
Hash tables are made up of two distinct parts:
- An array (something which we’re already familiar with)
- Hash function Assume we’ve to store these strings using Hash Table {‘Ada’, ‘Bea’, ‘Sam’, ‘Mia’}
Now we know internally hash table will use an array to store them. But, before storing the values directly in the array, we will pass this string one by one to the hash function.
What is Hash Function?
Think of term hash as used in cooking like a hash brown. We take raw ingredients, chop them and mix them all together. Our raw ingredients are data like strings in our example or something like a password or maybe an entire object. All we do is add this data to a hash function.
This hash function, in simplest term, will grind all data up and give us a simple and very smaller integer number.
There are few things that should be noted about hashing here:
- The hashing we will be doing in our example is not encryption.
- Also, hash functions are not reversible or invertible.
When we hash any information, we lose information about our raw ingredients. This is intentional. The motive here is that we cannot take any hash value result and try to turn it around to give us raw ingredients. Imagine, you've cooked hash brown and you want your raw ingredients like potatoes and onions back from it.
Now coming back to our example, the hash function will take a string value and gives us back an integer number based on some calculation.
This integer number is where we insert/add the value in the array.
Below is an example how Hash function calculates integer number for all strings we want to store in the array.
 Our String ‘Ada’ gets stored in an array at index number 2
Our String ‘Ada’ gets stored in an array at index number 2
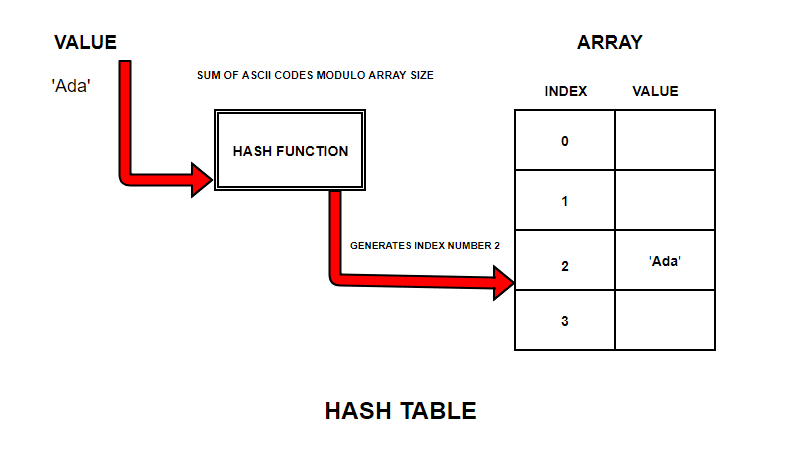 Now, let us try to store all the strings using the same calculation into the Hash table.
Now, let us try to store all the strings using the same calculation into the Hash table.
 The array is fully populated now. But, this time based on index numbers given by a calculation.
The array is fully populated now. But, this time based on index numbers given by a calculation.
Calculation used:
Index Number = Sum of ASCII Codes Modulo Size Of the Array
 Retrieving String From the Hash Table:
Retrieving String From the Hash Table:
Now, let’s try to retrieve string ‘Sam’ from this array.
We perform same calculation again.
1: Sum of ASCII code of each character
2: Perform Division
3: Get Remainder
And just like that, the remainder just gave an array index. We just found our angel which will always tell us what our index number is.
Thanks to Hash tables, the complexity of searching an element drops to O(1).
Associative Array Hash functions:
Just like our above example, the associative array uses a hash function too
But, the index number of an array is generated by ‘keys’. Let’s see how this below key-value pair gets stored in the hash table.
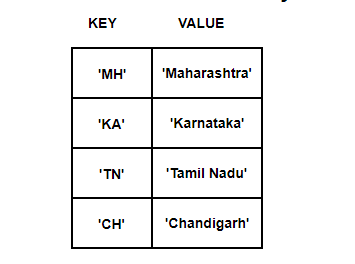
Here, keys like ‘MH’ are given to hash function to generate array integers.

Hash Collisions:
The above things happen in fairy tales or if it belongs to Happily-ever after Bollywood movie.
But, real life is not fair.
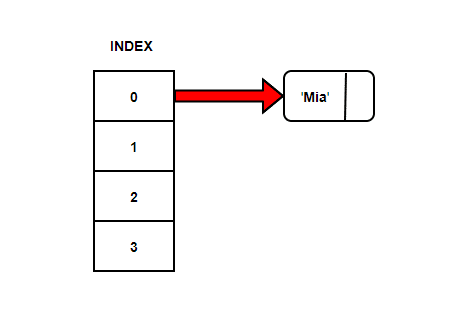
Assume we’ve to store strings in the hash table by using the hashing technique {“Mia”, “Tim”, “Bea”}. We’ll use the same sum of ASCII Code modulo array size calculation
 Wait, don’t we already have String ‘Mia’ at array position 0. How can we put ‘Bea’ in the same position?
Wait, don’t we already have String ‘Mia’ at array position 0. How can we put ‘Bea’ in the same position?
The keys have collided. Something we call as hashing collisions.
Collision Resolution Techniques:
There are many ways in which we can solve this collision thing-y.
Approach No 1- Linear Probing
(Also fondly known as Open addressing or Closed hashing)
An extremely simple solution. If the position of an array is occupied, always love thy neighbor i.e try to put the element in next position.
So, if we can’t put ‘Bea’ in position 0, try to put it in position 1.
But, our string ‘Tim’ already occupies position 1. Now what? Love Thy Neighbors Neighbor. Try position no 2.
Phew! We finally found an unoccupied spot. We can store ‘Bea’ here.
Placing an item in an unoccupied position of an array in case of collision is known as open addressing.
Every position is open to any item of an array. This is also called as linear probing as we perform a linear search to look for unoccupied space in case of collisions. If linear probing gets to the end of the array and still can’t find an empty position, it might cycle around from the beginning of the array and continue searching from there.
Finding An Element In Collision Affected Hash Tables:
Let’s say we want to find string ‘Bea’ in our Hash Table.
According to our index calculation, ‘Bea’ should’ve been at position 0. But, thanks to collisions, it had to take up a slot at position 3.
So, to search string ‘Bea’, we first go to the index calculated by the hash function, check if the element exists and if not, perform a linear search to see where the element resides.
Load Factor:
We were only dealing with 3 elements and we encountered a collision.
Imagine when we’re dealing with thousands of data, what will happen?
One way we can deal with this make the hash table bigger than needed to total amount of data we’re expecting. Something like only 70% of our hash table is ever occupied.
The ratio between the number of items stored to the size of the array is known as load factor.
Remember, when we were talking about arrays, we studied about a special type of arrays known as dynamic or re-sizable arrays.
If we’re implementing Hash tables with the dynamic arrays, it can be made to resize automatically if the above load factor reaches some threshold.
Fairy Tale Vs Real World:
In Fairy Tale, all the elements are stored in their respective indexes without any collision. This best case scenario gives us O(1) complexity.
But, in worst case scenario, we’re still looking at O(n) complexity where collisions force us to perform a linear search.
Approach No 2: Separate chaining:
(Also fondly known as Closed addressing or Open hashing)
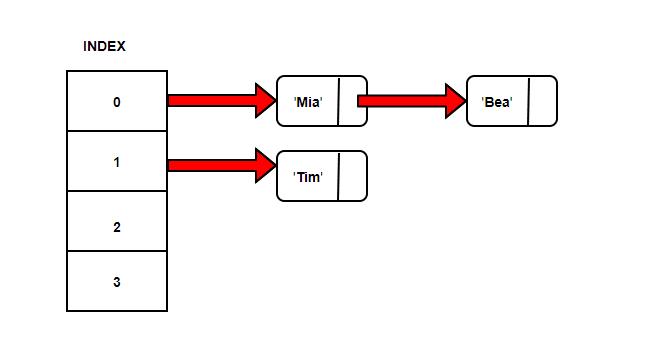
There’s another way to deal with the collision which is known as Separate chaining. Let’s try to populate our hash table again with Strings {“Mia”, “Tim”, “Bea”}.
If we calculate the index based on our sum of ASCII codes modulo array size, we get index as zero.
But, instead of storing string ‘Mia’ at position 0, we have got a pointer to the first node at the linked list.
What is a Linked List?
We’re going to study about the linked list in great detail soon but for now, think of it as a bunch of nodes that point to each other in one direction. An example would be that node A points to B and B points C.
Now, let’s try to store string ‘Tim’ with same calculation, the index comes out to be 1.
Again a pointer to a linked list from position 1.
Let’s try to store string ‘Bea’ now. The index number calculated is 0. So, ‘Bea’ is added to the linked list at position 0 and Node ‘Mia’ points to it.
Finding An Element In Collision Affected Hash Tables:
Let’s say we want to find string ‘Bea’ in our Hash Table.
Our index calculation tells ‘Bea’ should’ve been at position 0. We reach position 0 and then follow simple linked list traversal to find ‘Bea’.
At least with this technique, the index numbers where we store element given by hash functions remain unchanged. So the searching or lookup of an element is faster.
Sure, traversing a linked list also comes at some cost. The worst case complexity of traversing a linked list can be O(n).
So, what do we do? Hash tables were supposed to solve our beloved array search problem. We are still looking at O(n) complexity in most cases.
The power is all in the function:
You want a powerful hash table, all you need is a good hash function.
The hash function we used above, that is the sum of ASCII codes modulo array size was a bad one.
In any case, we have permutations of the same letters in the set, we will end up with the same value for the sum and leading same key which leads to disastrous collisions. Secondly, we need a good table size, preferably a prime number.
How do we pick a good hash function?
Picking a “good” hash function is absolutely necessary to successfully implementing a hash table. The storing and retrieving data in O(1) time comes down to answering the above question.
There are certain things which makes a hash function goody-goody.
- The most obvious one, it should avoid a collision as much as possible
- There should be a uniform distribution of value across hash table
- The function must be easy to compute.
Finding a “good” Hash Function:
A perfect hash function that is a function that has no collisions is an illusion.
But, better hash functions are not.
Let’s try a different hash function.
The index for a specific string will be equal to the sum of ASCII values of characters multiplied by their respective order in the string after which it is modulo with some prime number like 29.
 Here, each string will lead to a unique number, and with modulus a prime number, it is still possible that we may have collisions but maybe fewer collisions than when using a naive hash function like the sum of the characters.
Here, each string will lead to a unique number, and with modulus a prime number, it is still possible that we may have collisions but maybe fewer collisions than when using a naive hash function like the sum of the characters.
Supporting Hashing:
I know you might be wondering do I have to go off and write such complicated hash functions?
The answer is No.
Most programming languages give us a perfectly acceptable hash function which does all this heavy work for us.

Applications Of Hash Tables:
- Associative arrays have different names in various programming languages. They are implemented using Hash tables.
- The hash functions are used in various algorithms to make their updating and storing computing faster.
- Hash tables are used as disk-based data structures and database indexing.
- They can be used to implement caches mainly used to that are used to speed up the access to data.
- Several dynamic programming languages like Python, JavaScript, and Ruby use hash tables to implement objects.
- Hashing is a not just used in data structures, but also widely used in security, cryptography, graphics, audio.







